Spojité rozdelenia
Pre prácu s preddefinovanými rozdeleniami pravdepodobností je potrebné najskôr načítať knižnicu "distrib",čo realizujeme pomocou funkcie
`load()`kde ako argument uvedieme názov požadovanej knižnice. V našom prípade teda:
| (%i1) | load(distrib); |
Knižnica distrib obsahuje pre každé implementované rozdelenie množiny funkcií, potrebné pre pravdepodobnostné výpočty.
Volanie týchto funkcií sa skladá z dvoch častí. Prvú tvorí prefix, ktorý určuje druh požadovanej funkcie.
K dispozícii sú tieto prefixy:
| pdf_ | funkcia hustoty |
| cdf_ | distribučná funkcia |
| quantile_ | kvantilová funkcia |
| mean_ | stredná hodnota |
| var_ | rozptyl |
| std_ | smerodajná odchýlka |
| skeweness_ | koeficient šikmosti |
| kurtosis_ | koeficient špicatosti |
| random_ | náhodná hodnota premennej |
Druhú časť názvu funkcie, ktorá nasleduje bezprostredne za prefixom, tvorí meno (identifikátor) rozdelenia.
Vyberať môžeme z týchto spojitých rozdeleni:
| normal | Normálne rozdelenie | student_t | Studentovo t-rozdelenie | chi2 | Chí kvadrát rozdelenie | f | Fisherovo rozdelenie | exp | exponenciálne rozdelenie | lognormal | logaritmickonormálne rozdelenie | gamma | gama rozdelenie | continuous_uniform | spojité rovnomerné rozdelenie | logistic | logistické rozdelenie | pareto | Paretovo rozdelenie | weibull | Weibullovo rozdelenie | rayleigh | Rayleighovo rozdelenie | laplace | Laplaceovo rozdelenie | cauchy | Cauchyho rozdelenie | gumbel | Gumbelovo rozdelenie |
1 Rovnomerné rozdelenie
Náhodnými premennými s rovnomerným rozdelením sú napríklad chyby pri zaokrúhľovaní, doba čakania na výskyt určitej udalosti, ktorá sa opakuje v pravidelných intervaloch.
Príklad
Náhodná premenná $X$ má rovnomerné rozdelenie $\mathrm{Ro(-1,5)}$. Vypočítajte:
a) smerodajnú odchýlku,
b) pravdepodobnosť, že náhodná premenná $X$ sa bude odchyľovať od svojej strednej hodnoty najviac o $\pm\sqrt{3\mathbb{D}(X)}$
Riešenie
Smerodajnú odchýlku vypočítame buď priamo, použitím príslušnej funkcie:
| --> | std_continuous_uniform(-1,5); |
alebo môžeme tiež počítať postupne. Najskôr určíme strednú hodnotu. Podľa vzorca pre strednú hodnotu spojitej náhodnej premennej (pozri slajdy z prednášky č. 4, rovnica (11)). Zrejme funkcia hustoty rovnomerného rozdelenia $$ f(x)= \left\{ \begin{array}{ll} \frac{1}{6} & \mathrm{pre}\; -1 \lt x \lt 5\\ 0 & \mathrm{inak.} \end{array} \right. $$ Príslušný integrál teda budeme počítať len na intervale, kde je funkcia hustoty nenulová.
| --> | EX:integrate(1/6*x,x,-1,5); |
Rozptyl a následne smerodajnú odchýlku môžeme vypočítať priamo podľa vzorca (17) na uvedených slajdoch,teda
| --> | DX:integrate((x-EX)^2*1/6,x,-1,5); |
| --> | sigma:sqrt(DX); |
Druhou možnosťou je podľa rovnice (9) pre $k=2$ vypočítať začiatočný moment druhého rádu a rozptyl a následne smerodajnú odchýlku určiť podľa vzťahu (18)
| --> | EX2:integrate(x^2*1/6,x,-1,5); |
| --> | EX2-(EX)^2; |
| --> | sqrt(%); |
Pre potreby úlohy b) najskôr vypočítame
| --> | sqrt(3*DX); |
Tak dostávame $\mathbb{P}(-\sqrt{3\mathbb{D}(X)} \leq X-\mathbb{E}(X) \leq \sqrt{3\mathbb{D}(X)}=\mathbb{P}(-3 \leq X-2 \leq 3)=\mathbb{P}(-1 \leq X \leq 5)=$
| --> | integrate(1/6,x,-1,5); |
Príklad
Čas vymedzený na dokončenie určitej činnosti je náhodná premenná s rovnomerným rozdelením
od 30 do 40 minút. Aká je pravdepodonosť, že činnosť začínajúca sa o 12,00 hod. sa ukončí do 12,35?
Riešenie
Náhodná premenná $X$, ktorá vyjadruje čas dokončenia činnosti má rovnomerné rozdelenie $\mathrm{Ro}\left( \frac{1}{2},\frac{2}{3} \right)$
(30 min. = $\frac{1}{2}$ hod., 40 min. = $\frac{2}{3}$ hod.) a jej hustota pravdepodobnosti teda je
$$
f(x)= \left\{ \begin{array}{ll}
6 & \mathrm{ak} \; \frac{1}{2} \lt x \lt \frac{2}{3}\\
0 & \mathrm{inak.}
\end{array} \right.
$$
Ak si uvedomíme, že 35 min. = $\frac{7}{12}$ hod., a zoberieme do úvahy, kedy je hustota
pravdepodobnosti nenulová funkcia, tak pre hľadanú pravdepodobnosť $\mathbb{P}(\frac{1}{2} \leq X \leq \frac{7}{12})$ dostávame
| --> | integrate(6,x,1/2,7/12); |
2 Exponenciálne rozdelenie
Toto rozdelenie sa používa v teórii spoľahlivosti a životnosti, v teórii obnovy, v teórii hromadnej obsluhy
a v teórii dopravy. Opisuje sa ním doba životnosti niektorých zariadení, výrobkov, dĺžka trvania niektorých
aktivít alebo čakanie na určitú udalosť.
Významná je jeho súvislosť s Poissonovým rozdelením: Ak počet udalostí za určitú časovú jednotku sa riadi
Poissonovým rozdelením, tak doba čakania na výskyt ďalšej udalosti sa riadi exponenciálnym
rozdelením
2.1 Hustota exponenciálneho rozdelenia
Hustota exponenciálneho rozdelenia s parametrom $\lambda$ je určená vzťahom: $$ f(x) = \left\{ \begin{array}{ll} \lambda \, \mathrm{e}^{\lambda} & \mathrm{ak}\, x \gt 0\\ 0 & x \leq 0 \end{array} \right. $$
Zmeny tvaru funkcie hustoty môžeme pozorovať na nasledujúcom obrázku. Po vykonaní príkazu sa na ploche pracovného listu objaví graf. Po jeho aktivovaní myšou môžeme pomocou slidera v ponuke meniť jej vzhľad príp. nechať plynule prehrávať a pozorovať zmenu v závislosti od parametra. Hodnoty parametra $\lambda$ sú uložené v zozname d, ktorý generujeme príkazom makelist. V danom prípade sa jeho hodnoty plynule menia od jednotky po 4 s krokom 0.1.
| --> | with_slider_draw(d,makelist(i,i,10,40)/10,yrange=[ -1,4],xaxis=true,yaxis=true,explicit(pdf_exp(x,d),x,-1,5))$ |
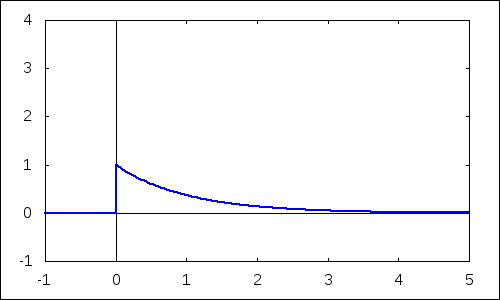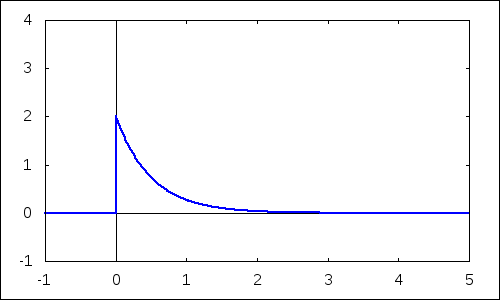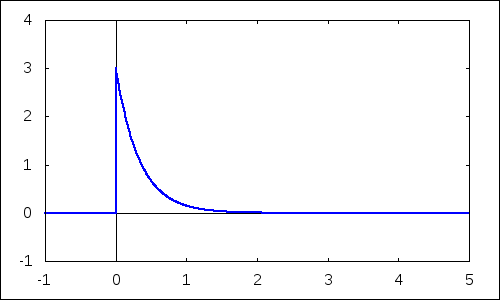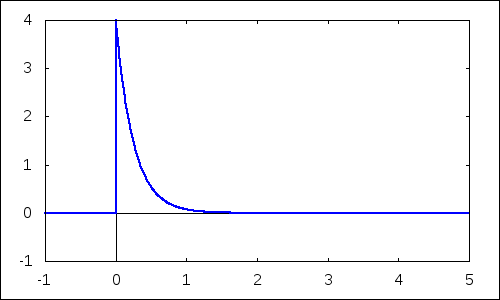
2.2 Distribučná funkcia
Podobne ako hustota aj distribučná funkcia bude nenulová len na intervale $x \gt 0$. Podľa známeho vzťahu (vzorec (3) na slajdoch č.4) dostávame pre distribučnú funkciu vyjadrenie:
| (%i10) | expand(integrate(d*exp(-d*t),t,0,x)); |
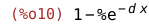
Distribučné funkcie, zodpovedajúce hustotám z predchádzajúceho odseku zobrazíme nasledujúcim príkazom:
| (%i12) | with_slider_draw(d,makelist(i,i,10,40)/10,yrange=[-0.5,1.5],xaxis=true,yaxis=true,explicit(cdf_exp(x,d),x,-1,5))$ |
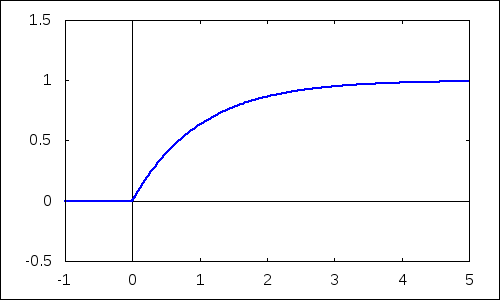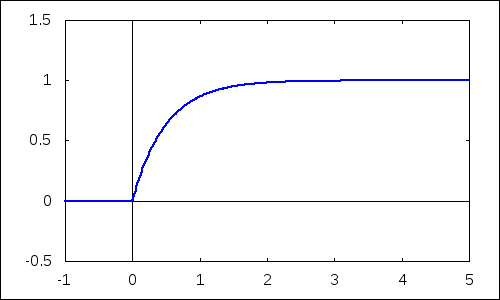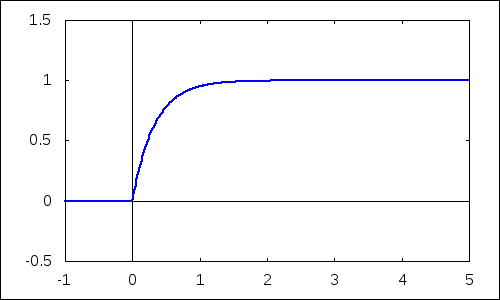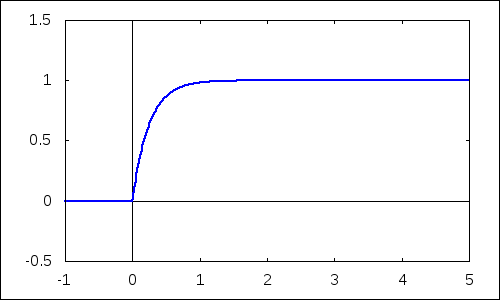
2.3 Charakteristiky exponenciálneho rozdelenia
Význam hodnoty parametra exponenciálneho rozdelenia je zrejmý ihneď po vyčíslení jeho charakteristík. Pre jeho strednú hodnotu dostávame:
| (%i16) | EX:integrate(x*d*exp(-d*x),x,0,inf); |

Podobne pre rozptyl postupne dostávame:
| --> | DX:integrate((x-EX)^2*d*exp(-d*x),x,0,inf); |

Príklad
Náhodná premenná $X$, ktorá sa riadi exponenciálnym rozdelením má
strednú hodnotu 4. Aká je pravdepodobnosť, náhodná premenná
nadobudne hodnotu z intervalu $(1,4)$?
Riešenie
V predchádzajúcich výpočtoch sme zistili, že stredná hodnota exponenciálneho
rozdelenia je rovná prevrátenej hodnote jeho parametra, teda $\frac{1}{\lambda}$. Teda $\frac{1}{\lambda}=4$
a teda $\lambda=\frac{1}{4}$. Príslušnú pravdepodobnosť určíme ako rozdiel hodnôt distribučnej
funkcie (pozri slajdy č.4, vzťah (2)).
| (%i18) | cdf_exp(4,1/4)-cdf_exp(1,1/4); |
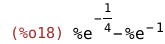
| (%i19) | float(cdf_exp(4,1/4)-cdf_exp(1,1/4)); |
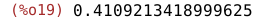
Príklad
Pravdepodobnosť, že doba čakania na obsluhu v určitej predajni bude kratšia ako 2 min.
je 0,16. Predpokladajme, že táto doba čakania sa riadi exponenciálnym rozdelením.
Určte strednú dobu čakania na obsluhu.
Riešenie
Podľa definície distribučnej funkcie (slajdy č.4, vzťah (1)) je pravdepodobnosť toho, že doba
čakania na obsluhu bude kratšia kao 2 minúty rovná hodnote distribučnej funkcie $F(2)$.
Dostávame teda rovnicu $F(2)=0,16$.
| (%i25) | parametre:float(solve(1-exp(-2*d)=0.16,d)); |

Hodnota neznámeho parametra exponenciálneho rozdelenia teda je
| (%i26) | d:rhs(parametre[2]); |
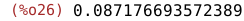
Hľadanú strednú dobu čakania teda určíme ako strednú hodnotu príslušného exponenciálneho rozdelenia
| (%i27) | mean_exp(d); |
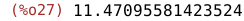
3 Normálne rozdelenie
Normálne rozdelenie má mimoriadny význam v teórii aj aplikáciách. Používa sa najmä v situáciách, kedy je konečný výsledok ovplyvnený veľkým počtom faktorov.
Náhodná premenná $X$, ktorá nadobúda hodnoty z celej množiny reálnych čísiel $\mathbb{R}$ má normálne rozdelenie $\mathrm{N}(\mu,\sigma^2)$ s parametrami $\mu$ a $\sigma^2$ ak jej hustota pravdepodobnosti má tvar $$ f(x) =\frac{1}{\sigma \sqrt{2\pi}}\mathrm{e}^{-\frac{1}{2}\left( \frac{x-\mu}{\sigma}\right)^2}. $$
Ilustrujeme si vplyv hodnoty jednotlivých parametrov na tvar funkcie hustoty resp. distribučnej funkcie normálneho rozdelenia. Použijeme k tomu funkciu 'with_slider_draw', ktorá umožňuje vytvárať animácie ovládané pomocou posuvníka.
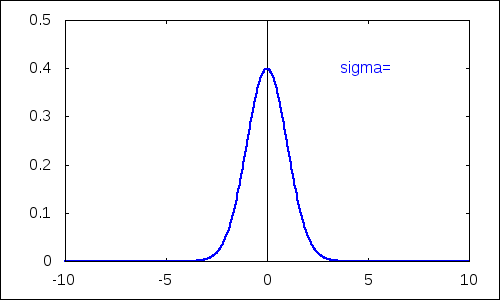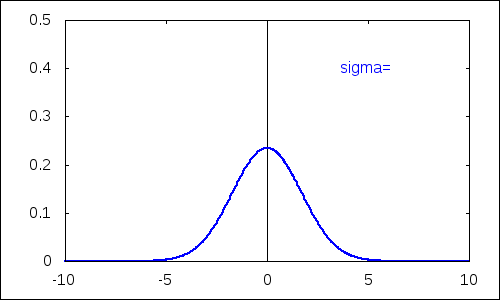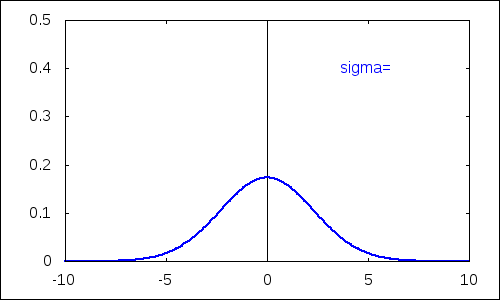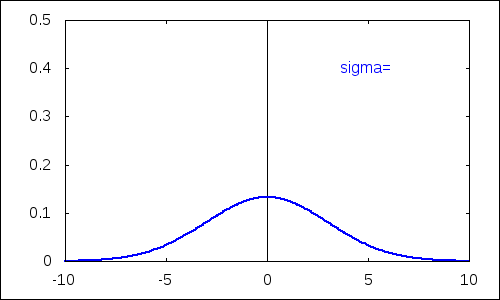
Najskôr vplyv parametra $\sigma^2$, ktorý určuje rozptyl náhodnej premennej.
| (%i15) |
with_slider_draw( d,/*názov premenej riadenej posuvníkom*/ makelist(i,i,10,30)/10,/*vygenerovanie zoznamu hodnôt*/ yrange=[0,0.5],/*rozsah hodnôt y*/ xaxis=true,yaxis=true,/*zobrazenie súradnicových osí*/ line_width=2, label(["\sigma=",5,0.4]), explicit(pdf_normal(x,0,d),x,-10,10) ); |
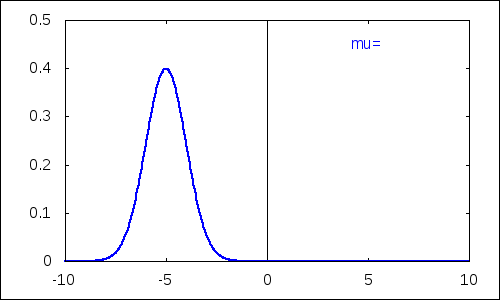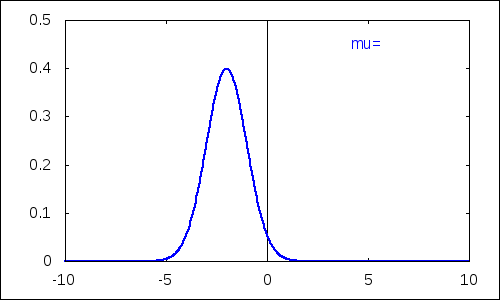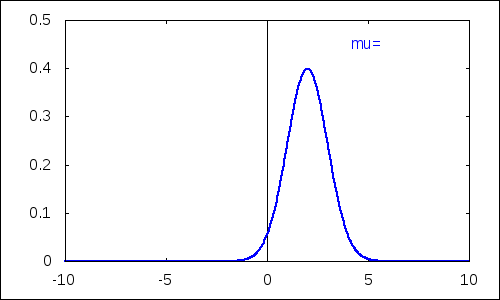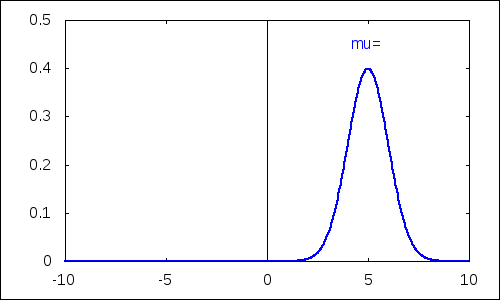
Parameter $\mu$ plní funkciu strednej hodnoty.
| (%i18) |
with_slider_draw( d,/*názov premenej riadenej posuvníkom*/ makelist(i,i,-5,5),/*vygenerovanie zoznamu hodnôt*/ yrange=[0,0.5],/*rozsah hodnôt y*/ xaxis=true,yaxis=true,/*zobrazenie súradnicových osí*/ line_width=2, label(["\mu=",5,0.45]), explicit(pdf_normal(x,d,1),x,-10,10) ); |